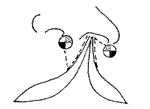
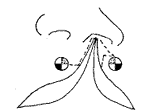
Millard法中,C瓣末端点向裂隙侧水平方向延伸的距离与鼻小柱基部设计的切口止点(圆心点)的位置有关,在同一垂线方向上,切口止点愈近鼻小柱基部,则C瓣向患侧鼻底延伸的距离愈长。而在同一水平方向上,切口止点(圆心点)距离C瓣末端愈近,C瓣向患侧鼻底延伸的距离愈长,参见图4、5。
3 讨 论
3.1 Millard法手术设计上的特点
Millard法的设计特点是将健患侧唇上能使唇峰点下降的切口止点定得远离裂隙侧唇峰点,从而可以使裂隙侧唇峰点有最大限度的旋转下降,以此来恢复两侧唇弓的对称性。根据本研究结果,不难看出,灵活掌握本法的要领在于根据不同畸形特征(主要是健患侧唇峰的高度差),在手术中确定鼻小柱基部和患侧鼻翼下方的定点。如图6示,若将上述两点分别定在图中的黑色象限,可最大限度地使裂隙侧唇峰点旋转下降,反之,若定在图中的虚线象限内,则可控制裂隙侧唇峰点的下降距离。这恰好解释了为什么同一手术方法,可以在一定范围内适用于具有不同畸形程度的病例,同时也说明了同一手术方法受术者临床经验不同的影响,可以获得迥然不同的术后效果。
图6 Millard法定点区域示意图
3.2 Tennison-Randall法手术设计上的特点
Tennison-Randall法有效地利用了本研究方法1的几何学原理,使裂隙侧唇峰旋转下降的圆心点(切口止点)降到了最低限度,从而可以自如地使裂隙侧唇峰点下降,其下降的距离,取决于术者对两侧切口止点的选择。如图7示,将切口止点确定在图中的黑色象限内,则可以获得最大限度的唇峰点的旋转下降,相反,选择在图中的虚线象限内,则可控制裂隙侧唇峰点的下移。当然,同Millard法的应用一样,这种感觉与预测能力只有在临床实践中反复揣摩才能获得。而以本文的研究结果作为唇裂修复术式设计的基本理论,则可以有针对性地去指导术者的临床实践,减少积累临床经验过程中的盲目性,提高对术后效果的预见能力。
图7 Tennison-Randall法定点区域示意图
3.3 Millard法与Tennison-Randall法的比较
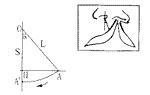
虽然两法设计的切口部位不同,但均是为了使裂隙侧唇峰点下移,达到与健侧对称的目的。因此,为了进一步比较两种方法对裂隙侧唇峰高度的下降程度,笔者特做如下模拟:在Millard法设计中,鼻小柱基部(O点)至健侧裂隙侧唇峰(A点)的距离为L,O点至A点的连线与垂线所成的夹角为α(图8),则A点高度可下降的距离为H,H=L-s=L-L·cos α=L(1-cos α),设L分别为6、8、10 mm,α分别为30°或45°时,结果见表1。
图8 计算唇峰点在Millard法下降距离示意图
表1 Millard法中健侧唇的裂隙侧唇峰点高度
在不同条件下的最大下降距离(mm)
| 角度(α) | 切口长度(L | ||
| 6 | 8 | 10 | |
| 30° | 0.804 | 1.072 | 1.340 |
| 45° | 1.758 | 2.344 | 2.930 |
即使以Millard本人的图示为例图9[2],转折切口长度为3 mm,鼻小柱基部点至健侧裂隙唇峰点的距离为7 mm(3 mm+4 mm),因两切口间呈90°夹角,所以转折切口末端与裂隙侧唇峰点的距离则为7.6 mm(32+72),假设转折切口止点与裂隙侧唇峰点的连线与垂线呈30度角时,则唇峰点高度的最大下降距离为1.0184 mm,呈45°角时,为2.2268 mm,呈60°角时,唇峰点高度的最大下降距离也仅为3.3 mm。同法,在Tennison-Randall法的设计中,假设从裂隙侧唇峰点(A点)向健侧人中嵴所作的切口长度为L(图10),切口止点为O点,切口线与垂线间的夹角为α,裂隙侧唇峰点高度可下降的最大距离为H,则H=L+s=L+L·cos α=L(1+cos α),设L分别为2、3、4 mm,α分别为60°、75°、90°,则结果见表2。
表2 Tennison-Randall法中健侧唇的裂隙侧唇峰点高度
在不同条件下的最大下降距离(mm)
| 角度(α) | 切口长度(L) | ||
| 2 | 3 | 4 | |
| 90° | 2.000 | 3.000 | 4.000 |
| 75° | 2.517 | 3.776 | 5.035 |
| 60° | 3.000 | 4.500 | 6.000 |
相关阅读:
 发表评论
发表评论 用户评论
用户评论