摘　要：目的:探讨Millard法与Tennison-Randall法在单侧唇裂修复手术中蕴藏的几何学原理。方法:对两法的手术设计进行详细的几何学解析。结果:Millard法的特点是在水平方向上,将能使裂隙两侧唇峰点旋转下降的轴心点距唇峰点较远;而Tennison-Randall法则是在垂直方向上,将能使裂隙侧唇峰点旋转下降的轴心点形成的位置较低。结论:Millard法的设计更符合对唇裂修复的生理性原则,而Tennison-Randall法更符合修复唇裂的几何学条件,并认为这是两法能长期并存而未被相互取代的内在机制。

　　虽然Tennison-Randall法与Millard法较其它方法可以使唇裂患者更好地恢复上唇形态,但国

　　1　材料和方法

　　1.1　材料

　　用圆规、量角器、直尺等测量工具,在单侧唇裂图形上模拟Tennison-Randall法和Millard法的切口设计,以裂隙两侧唇峰点的旋转下降距离作为观测指标,进行比较观察。其中健侧唇的裂隙侧唇峰点以健侧唇峰点至人中凹的距离标定,患侧唇的裂隙侧唇峰点以健侧唇峰至口角的距离标定。

　　1.2　方法

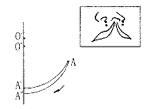
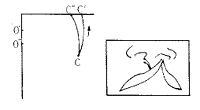
　　①O′、O″点分别为同一垂线上的两个圆心点,A为垂线外下的一点,当分别以O′和O″点为圆心向下旋转时,观察A点的最大下降距离。设A点为裂隙侧唇峰点,O′、O″点为鼻小柱基部下方或患侧鼻翼基部下方的定点,则可以发现将能使唇峰点(A)旋转的圆心点(O′、O″)定得愈低,则唇峰点的下降距离愈大(图1)。

图1 方法①几何学原理示意图

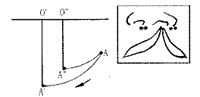
　　②O′、O″点分别为同一水平线上的两个圆心点,A为与O′、O″点同侧外的点,分别以O′和O″点为圆心将A点向下旋转时,则可以发现圆心点距A点距离愈远时,A点的下降距离愈大。设O′、O″点为鼻小柱基部或患侧鼻翼基部的定点,A点为裂隙侧唇峰点,则上述两处定点距唇峰点的距离愈远,唇峰点的下降距离愈大(图2)。

图2 方法②几何学原理示意图

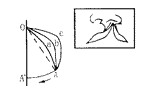
　　③O点为圆心,A点为旋转点,分别以a、b、c 3种连线形式作切开,可以发现A点的最大下旋距离不变。设O点为鼻小柱基部或患侧鼻翼基部的定点,A点为裂隙侧唇峰点,则唇峰点的下降距离与唇峰点和上述两点的连线形式无关(图3)。

图3 方法③几何学原理示意图

　　④O′、O″仍为同一水平线上的两个圆心点,C为两点同侧外的点,分别以O′、O″点为圆心,将C点向上方旋转,则可以发现,C点距圆心点的距离愈近,则在水平方向上延伸的距离愈长。设O′、O″点为鼻小柱基部的定点,C点为Millard法设计中C瓣的末端点,则鼻小柱基部点距C瓣末端点的距离愈近,C瓣向患侧鼻底延伸的距离愈大(图4)。

图4 方法④几何学原理示意图

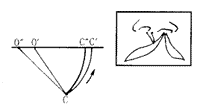
　　⑤O′、O″为同一垂线上的两点,C为上述两点同侧外的一点,分别以O′、O″点为圆心,将C点向上旋转时,则可以发现,圆心点距离愈远,C点在水平方向上的延伸距离愈长。设O′、O″为鼻小柱基部下方的定点,C点为Millard法设计中C瓣的末端点,则鼻小柱基部定点愈高,C瓣向患侧鼻底延伸的距离愈大(图5)。

图5 方法⑤几何学原理示意图

　　2　结　果

　　裂隙侧唇峰点旋转下降的距离与切口止端形成的圆心点的位置有关,在同一垂线方向上,圆心点的位置愈低,则唇峰点可旋转下降的最大距离愈大。而在同一水平方向上,圆心点距裂隙侧唇峰点的距离愈远,当以两点间距离为半径时,可使裂隙侧唇峰点的下降距离愈大,参见图1、2。

　　裂隙侧唇峰点的下降距离只与能使该点旋转下降的切口止点(圆心点)的位置有关,而与两点间的线连形状无关,参见图3。